FAQ 2006-04.1:
the integrals of
my spectrum make no sense, what is wrong ?
This question leads to a couple of other issues such as
1D-TROESY and Ernst
angle
Department of Chemistry,
University of Alberta May
2006
NMR News 2006-04
News and tips from the NMR support group for users of the Varian NMR systems in the
Department
Editor: Albin.Otter@ualberta.ca
http://nmr.chem.ualberta.ca
There are no fixed publishing dates for this newsletter; its appearance solely depends on whether there is a need to present information to the users of the spectrometers or not.
Other content of this NMR News is no longer meaningful and has been removed May 2010.
Contents
|
|
|
|
|
FAQ 2006-04.1:
the integrals of
my spectrum make no sense, what is wrong ? |
|
NMR staff changes The new technologist, Nupur Dabral, will join the NMR team on June 1. Nupur comes to us from Raylo/Degussa. She can be reached in WB-13 (2573). |
FAQ 2006-04.1: the integrals of my spectrum make no sense, what is wrong?
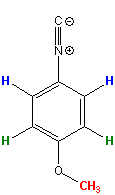 Relaxation
is not only important for human beings, it is essential for NMR spectroscopy
but, typically, NMR users do not care much about any form of
relaxation in their NMR spectrum until
something does not quite work out. A fairly common case is integrals
that do
not make sense like in the example shown here. 1.2 and 1.5 protons are
hard to imagine, short of splitting atoms. The molecule used as an example
here
(p-methoxy-phenylisonitrile *) is shown on the
left. Clearly, it should produce integrals in a
2 : 2 :
3 ratio. In other words, there is an
integral "deficit" of 40% and 23% respectively in this
spectrum for the protons shown in blue and
green. The spectrum was recorded with a total relaxation delay of 5 sec
which is the default on our spectrometers and sufficient in most, but not
all cases as this example shows. Relaxation
is not only important for human beings, it is essential for NMR spectroscopy
but, typically, NMR users do not care much about any form of
relaxation in their NMR spectrum until
something does not quite work out. A fairly common case is integrals
that do
not make sense like in the example shown here. 1.2 and 1.5 protons are
hard to imagine, short of splitting atoms. The molecule used as an example
here
(p-methoxy-phenylisonitrile *) is shown on the
left. Clearly, it should produce integrals in a
2 : 2 :
3 ratio. In other words, there is an
integral "deficit" of 40% and 23% respectively in this
spectrum for the protons shown in blue and
green. The spectrum was recorded with a total relaxation delay of 5 sec
which is the default on our spectrometers and sufficient in most, but not
all cases as this example shows.
The five spectra below were recorded with increasingly longer total relaxation delays as indicated in the yellow text: 5 sec, 10 sec, 20 sec, 40 sec and finally 100 sec. The total relaxation time is the sum of the acquisition time (at) and any relaxation delays such as d1. |
| Summary: the peaks at 6.3 ppm need between 20 and 40 sec to integrate properly while the signal at 6.8 ppm requires even longer: 40 sec is not enough but 100 seconds works! The need for such long delays is fortunately the exception but raises the question how long the T1 relaxation times really are in this molecule? |
|
T1-Relaxation in NMR Without going into details, there are two types of relaxation in NMR: T1-relaxation (also called longitudinal or spin-lattice relaxation) and T2-relaxation (also called transverse or spin-spin relaxation). In a nutshell, T1-realxation is the process that brings the magnetization vector back to the z-dimension (= thermodynamic equilibrium) after a radio frequency pulse turned the vector into the x,y plane. Only magnetization in the x,y plane can be recorded. Measuring T1 values is not a problem as long as the correct pulse sequence is used (shown below): |
||||||||||||||||||||||||||||||||||||
|
Note the huge 80 sec d1 relaxation delay: it is important to apply the pulses to a fully relaxed spin system. p1 is a 180 deg pulse, pw is a 90 deg pulse. The delay d2 in between is incremented from a very short time (125 msec) to over two minutes (128 sec). This technique is called inversion recovery, an expression that is self-explanatory by looking at the set of spectra below. The T1 relaxation process is what makes the signals recover from negative peaks to positive ("normal") peaks. |
||||||||||||||||||||||||||||||||||||
|
Without any mathematical analysis whatsoever, it can be seen easily that the methyl peak at 3 ppm recovers much faster than the other two: at d2 = 4 the methyl signal is already positive while the two aromatic signals are still negative. At d2 = 8 and d2 = 16 it can be seen that the left one of the two aromatic peaks is recovering slower (longer T1) than the right one. The last two spectra are nearly identical, indicating that after more than a minute the relaxation is basically complete. |
||||||||||||||||||||||||||||||||||||
|
The VNMRJ software can analyze the recovery of the peaks in a precise manner as shown above. It is evident that the process is far from linear: it is an exponential process. The blue line (# 5) is from the methyl group, number 1 and 2 are from the peaks at 6.8 ppm and 3 and 4 are from the 6.3 ppm signal. The numerical result from the exponential analysis (T1 values in seconds):
Looking, for example, at the blue # 5 curve, it can be seen clearly that it takes far more than one T1 period (5.3 sec in this case) of relaxation to get the full signal intensity back after each transient. Based on this exponential relaxation behavior it can be calculated how much of the signal will be recorded after the first pulse (which is the only one that gives 100.0% signal!). For various ratios of (relaxation / T1) the numbers are as follows:
This Table shows clearly that in the spectrum with the 5 sec relaxation delay the peaks at 6.8 ppm had only about 0.23 T1 periods of relaxation (5 sec for d1+at divided by the 22.2 sec for T1). The reason that they did not integrate even worse than the observed -40%, is the fact that the methyl group itself, taken as an integration reference, had only 1.0 T1 relaxation period and for this reason was not at full intensity/integral either. If the methyl group had a T1 of only 1 sec, and consequently produced >99% of its maximum attainable intensity/integral, then the integration error on the 6.8 ppm signal would have been -78%. In the 100 sec relaxation spectrum all signals had more or just about 5 T1s to recover and hence the integrations worked out very well. It is important to note
that not only the integral is too low with insufficient relaxation, the NMR
peaks themselves suffer from the same problem. However, the latter problem
is typically far less obvious to the human eye than integral numbers
like the ones shown in the first spectrum
because we are used to see very different signal intensities based on
splitting of the signals by coupling constants. |
||||||||||||||||||||||||||||||||||||
 For
those few who have not yet given up reading, there is one more interesting
aspect to this. Which proton pair, the blue
one or the green one is the one with the super
slow T1? This is not a trivial question at all and leads immediately to
another question: why are the relaxation times so long in the first
place? For
those few who have not yet given up reading, there is one more interesting
aspect to this. Which proton pair, the blue
one or the green one is the one with the super
slow T1? This is not a trivial question at all and leads immediately to
another question: why are the relaxation times so long in the first
place?In general, protons that are in close proximity of other protons, ideally many of them, have short T1s. The other way around, protons which are somewhat isolated from other protons have long T1s. Based on this, the green protons, next to the methyl group, should be the ones at 6.3 ppm (T1 12.8 sec) whereas the blue ones, ortho to the isonitrile group, should be the ones at 6.8 ppm with the 22.2 sec T1. Instead of guessing, this can also be verified experimentally: proximity in space can be measured by means of NOEs! The structure is repeated here for convenience. It is identical to the one shown above. |
||||||||||||||||||||||||||||||||||||
|
This NOE spectrum (also called 1D-TROESY) obtained by selective excitation of the methyl group at 3 ppm, confirms this entirely! The NOE to the protons at 6.3 ppm is more than 10 times stronger than the one to the other two protons. The 6.3 ppm signal is created by the green protons ortho to the methoxy group. The methoxy group helps with the relaxation whereas on the isonitrile side there is no such "relaxation help" available. |
* Sample and data were kindly provided by Jason Norman (Prof. Stryker's research group). Thanks Jason!
|
Ernst angle It is generally known that the signal/noise ratio in an NMR experiments increases with the square root of the number of transients (nt). However, if there is not sufficient relaxation the expected improvement will not happen. In an extreme case, in a given time, say 1 minute, 5 transients with 12 seconds total relaxation time may produce a better s/n than 30 transients with only 2 sec total relaxation: it all depends on T1! Alternatively, the pulse angle can be reduced from 90 deg to allow faster pulsing without creating an insufficient relaxation situation. In other words, there is an optimum of relaxation and pulse angle which is known as the Best Pulse Angle or Ernst angle. If the T1 is known, the Ernst angle b can be calculated by the formula shown here (a scientific calculator does that easily): |
|
| In the example discussed
above, for a 22.2 sec maximum T1 and a value of 5.0 sec for d1+at, the Ernst
angle is 37.0 deg. For d1+at = 10 sec the best pulse angle would
be 50.4 deg and the resulting spectrum identical to the one with the 5.0
sec/ 37 deg combination. There are obviously many more combinations possible
that would give the same end result. The concept of a reduced pulse angle (<90 deg) cannot be applied to all techniques. Many 2D experiments require precise 90 deg pulses. Furthermore, if the T1 is not known, the best pulse angle cannot be calculated. Measuring T1 first will take more time than the actual experiment itself which is why the practical importance of this is somewhat limited and the reason it is shown only as footnote. |